Question

A beam of electrons is accelerated across a potential of 14.60 kV before passing through two slits. The electrons form an interference pattern on a screen 4.40 m in front of the slits. The first-order maximum is 8.80 mm from the central maximum. What is the distance between the slits

Answer 1

`5.08* 10^(-9)\ \text{m}`

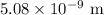
Step-by-step explanation:

h = Planck constant =
`6.626* 10^(-34)\ \text{Js}`

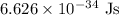
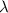`\lambda` = Wavelength

m = Mass of electron =
`9.11* 10^(-31)\ \text{kg}`

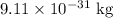
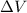`\Delta V` = Potential difference = 14.6 kV

e = Charge of electron =
`1.6* 10^(-19)\ \text{C}`

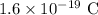
d = Distance between slits

`\sin\theta=(8.8* 10^(-3))/(4.4)`

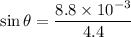
We have the relation

`(h)/(\lambda)=√(2me\Delta V)\\\Rightarrow \lambda=(h)/(√(2me\Delta V))\\\Rightarrow \lambda=\frac{6.626* 10^(-34)}{\sqrt{2* 9.1* 10^(-31)* 1.6* 10^(-19)* 14.6* 10^3}}\\\Rightarrow \lambda=1.016* 10^(-11)\ \text{m}`

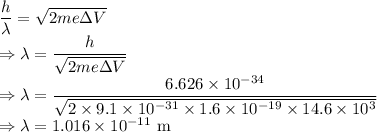
Wavelength is given by

`d\sin\theta=\lambda\\\Rightarrow d=(\lambda)/(\sin\theta)\\\Rightarrow d=(1.016* 10^(-11))/((8.8* 10^(-3))/(4.4))\\\Rightarrow d=5.08* 10^(-9)\ \text{m}`

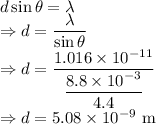
The distance between the slits is
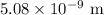`5.08* 10^(-9)\ \text{m}`.