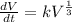The rate of change of the volume V of water in a tank with respect to time t is directly proportional to the cubed root of the volume. Write a differential equation that describ…

Question

asked Jul 21, 2022 30.7k views

1 Answer

Crezzur · Answer 1 · 2022-07-27T06:46:46+0000

Answer:

The differential equation becomes -

$(dV)/(dt) = k\sqrt[3]{V}$ i.e.
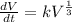
$(dV)/(dt) = kV^{(1)/(3) }$

Explanation:

Given - The rate of change of the volume V of water in a tank with respect to time t is directly proportional to the cubed root of the volume.

To find - Write a differential equation that describes the relationship.

Proof -

Rate of change of volume V with respect to time t is represented by
(dV)/(dt)

Now,

Given that,

The rate of change of the volume V of water in a tank with respect to time t is directly proportional to the cubed root of the volume.

⇒
(dV)/(dt) ∝
$\sqrt[3]{V}$

Now,

We know that, when we have to remove the Proportionality sign , we just put a constant sign.

Let k be any constant.

So,

The differential equation becomes -

$(dV)/(dt) = k\sqrt[3]{V}$ i.e.
$(dV)/(dt) = kV^{(1)/(3) }$