Question

The design of a 60.0 cm industrial turntable requires that it has a kinetic energy of 0.250 j when turning at 45.0 rpm. What must be the moment of inertia of the turntable about the rotation axis

Answer 1

The moment of inertia of the turntable about the rotation axis is 0.0225 kg.m²

Step-by-step explanation:

Given;

radius of the turnable, r = 60 cm = 0.6 m

rotational kinetic energy, E = 0.25 J

angular speed of the turnable, ω = 45 rpm

The rotational kinetic energy is given as;

`E_(rot) = (1)/(2) I \omega ^2`

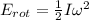
where;

I is the moment of inertia about the axis of rotation

ω is the angular speed in rad/s

`\omega = 45 (rev)/(\min) * (2 \pi \ rad)/(1 \ rev) * (1 \ \min)/(60 \ s) \\\\\omega = 4.712 \ rad/s`

`E = (1)/(2) I \omega ^2\\\\I = (2E)/(\omega ^2) \\\\I = (2 \ * \ 0.25)/((4.712)^2) \\\\I = 0.0225 \ kg.m^2`

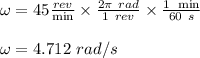
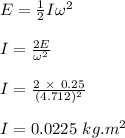
Therefore, the moment of inertia of the turntable about the rotation axis is 0.0225 kg.m²