Question

Suppose that 158 out of a random sample of 200 letters mailed in the United States were delivered the day after they were mailed. Based on this, compute a 90% confidence interval for the proportion of all letters mailed in the United States that were delivered the day after they were mailed. Then find the lower limit and upper limit of the 90% confidence interval.

Answer 1

The 90% confidence interval for the proportion of all letters mailed in the United States that were delivered the day after they were mailed is (0.7426, 0.8374). The lower limit is 0.7426 while the upper limit is of 0.8374.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

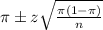
In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

Suppose that 158 out of a random sample of 200 letters mailed in the United States were delivered the day after they were mailed.

This means that
`n = 200, \pi = (158)/(200) = 0.79`

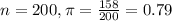
90% confidence level

So
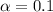`\alpha = 0.1`, z is the value of Z that has a p-value of
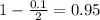`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

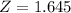The lower limit of this interval is:

`\pi - z\sqrt{(\pi(1-\pi))/(n)} = 0.79 - 1.645\sqrt{(0.79*0.21)/(200)} = 0.7426`

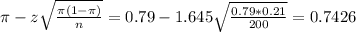
The upper limit of this interval is:

`\pi + z\sqrt{(\pi(1-\pi))/(n)} = 0.79 + 1.645\sqrt{(0.79*0.21)/(200)} = 0.8374`

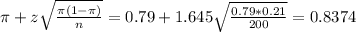
The 90% confidence interval for the proportion of all letters mailed in the United States that were delivered the day after they were mailed is (0.7426, 0.8374). The lower limit is 0.7426 while the upper limit is of 0.8374.