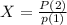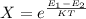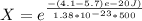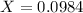Question

A two-state system is in an environment at temperature 500 K. The energy of state 1 is 4.1e-20 J, and the energy of state 2 is 5.7e-20 J. Let be the probability of finding the system in state 1, and be the probability of finding the system in state 2. What is the ratio

Answer 1

Complete Question

A two-state system is in an environment at temperature 500 K. The energy of state 1 is
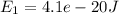`E_1=4.1e-20 J`, and the energy of state 2 is
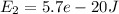`E_2= 5.7e-20 J`. Let P(1) be the probability of finding the system in state 1, and be the probability of finding the system in state 2. What is the ratio P(2)/P(1)

Answer:

`X=0.0984`

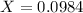
Explanation:

From the question we are told that:

Temperature T=500 K

Energy of state 1
`E_1=4.1e-20 J`,

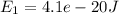Energy of state 2 is
`E_2= 5.7e-20 J`

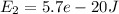
Generally the equation for Probability of finding the system in state is mathematically given by

`P(1)=e ^{(-E_1)/(KT)}`

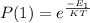
Therefore

For Probability of finding the system in state 1
`P(1)`

`P(1)=e ^{(-E_1)/(KT)}`

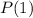
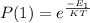
Where

K is Boltzmann constant

`K=1.38*10^(-23)`

`P(1)=e ^{(-(4.1e-20 J))/(1.38*10^(-23)*500)}`

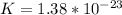
For Probability of finding the system in state 1
`P(2)`

`P(2)=e ^{(-(5.7e-20 J))/(1.38*10^(-23)*500)}`

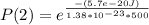
Generally the equation for The Ratio of
`P(2)` and
`P(2)` is mathematically given by

`X=(P(2))/(p(1))`

`X=e ^{(E_1-E_2)/(KT)}`

`X=e ^{(-(4.1-5.7)e-20 J))/(1.38*10^(-23)*500)}`

`X=0.0984`