Answer:
a) the maximum number of phases that can exist in equilibrium is
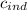 + 2
+ 2
b) the number of independent components in this system are 6
Step-by-step explanation:
We know that, The degree of freedom f for a system can be simply referred to as number of variables that must be defined to completely solve a system.
If degree of freedom is 0, then any problem is can be solved.
a) If a system has cind independent components, what is the maximum number of phases that can exist in equilibrium?
The degree of freedom for a system can be written as;
f =
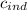 - p + 2
- p + 2
where f is the degree of freedom
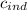 is the number of independent component
is the number of independent component
so we solve for
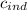
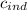 = f + p - 2
= f + p - 2
we know that f can not be less than 0
Hence maximum possible face will be;
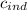 = p - 2
= p - 2
p =
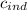 + 2
+ 2
Therefore, the maximum number of phases that can exist in equilibrium is
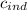 + 2
+ 2
b) A given system has eight liquid phases in equilibrium with each other. What must be true about the number of independent components in this system?
Number of phases in the system p = 8
p =
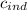 + 2
+ 2
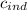 = p - 2
= p - 2
we substitute
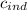 = 8 - 2
= 8 - 2
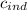 = 6
= 6
Therefore, the number of independent components in this system are 6