Question

An electron has a mass of 9.109 x 10 kg. A positron is a positively charged particle with the same mass as an electron. When an electron and positron collide, they annihilate to convert all their mass into energy. . How much energy is released by the reaction of 1 mole of electrons and a positrons

Answer 1

It is released 6.16x10²⁹ eV in an annihilation reaction between 1 mol of electron and 1 mol of positrons.

Step-by-step explanation:

We can find the energy of 1 electron as follows:

`E_(e) = mc^(2)`

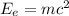
Where:

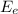`E_(e)`: is the energy of the electron

m: is the mass = 9.109x10⁻³¹ kg

c: is the speed of light = 3.0x10⁸ m/s

Hence, the energy is:

`E_(e) = mc^(2) = 9.109\cdot 10^(-31) kg*(3.0\cdot 10^(8) m/s)^(2) = 8.19 \cdot 10^(-14) J*(1 eV)/(1.602\cdot 10^(-19) J) = 511.2 keV`

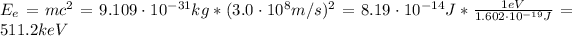
Since the mass of a positron is the same as the electron, the energy produced by one positron is the same that the energy produced by one electron, that is to say, 511 keV. By conservation of energy and momentum, we have 1.022 MeV of energy produced by the annihilation between a positron and an electron.

Hence, the energy produced for 1 mol of electrons (6.022x10²³ electrons) or positrons is:

`nE_(e) = (511.2 keV)/(1 e^(-))*6.022 \cdot 10^(23) e^(-) = 3.08 \cdot 10^(29) eV`

The same amount of energy (3.08x10²⁹ eV) is produced by one mol of positrons (because the mass of a positron is equal to the mass of an electron). Again, by conservation of energy and momentum, the total energy produced by the annihilation of 1 mol of positrons and 1 mol of electrons is 6.16x10²⁹ eV.

Therefore, it is released 6.16x10²⁹ eV in an annihilation reaction between 1 mol of electrons and 1 mol of positrons.

I hope it helps you!