This question is incomplete, the complete question is;
According to a recent survey, 73% of all customers will return to the same grocery store. Suppose 14 customers are selected at random, what is the probability that: (Round probabilities to 4 decimal places and the expected customers to 2 decimal places)
a) All 14 will return?
b) How many customers would be expected to return to the store ?
Answer:
a) the probability that All 14 will return is 0.0122
b) The number of customers that would be expected to return to the store is 13.27
Explanation:
Given the data in the question;
p = 73% = 0.73
sample size n = 14
a) the probability that All 14 will return;
P( x = 14 ) = ⁿCₓ × Pˣ ×

we substitute
P( x = 14 ) = ¹⁴C₁₄ × (0.73)¹⁴ ×

P( x = 14 ) = [ 14! / ( 14! × ( 14 - 14)!) ] × (0.73)¹⁴ ×
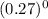
P( x = 14 ) = 1 × 0.0122045 ×
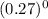
P( x = 14 ) = 1 × 0.0122045 × 1
P( x = 14 ) = 0.0122045 ≈ 0.0122 { 4 decimal place }
Therefore, the probability that All 14 will return is 0.0122
b) Expected Customers;
E(x) = n × p
we substitute
E(x) = 14 × 0.73
E(x) = 13.27 { 2 decimal place }
Therefore, The number of customers that would be expected to return to the store is 13.27