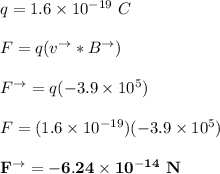Question

An electron that has an instantaneous velocity of is moving through the uniform magnetic field (a) Find the force on the electron due to the magnetic field. (b) Repeat your calculation for a proton having the same velocity

Answer 1

Step-by-step explanation:

From the given information:

The missing value are as follows:

The velocity
`v ^(\to) = (2.0 * 10^6 \ m/s) \hat i + (3.0 * 10^6 \ m.s) \hat j`

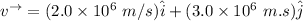
The uniform magnetic field
`B^(\to) = (0.030 T)\hat i -(0.15 T) \hat j`

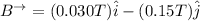
The force on electron as a result of the Magnetic field is:

`F^\to = q(v^\to * B^\to)`

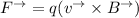
here;

Change of electron
`q = -1.6 * 10^(-19) C`

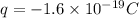
Then,

`v^(\to) * B^(\to) = \left|\begin{array}{ccc}2*10^6&3* 10^6&0\\0.03&-0.15&0\end{array}\right|`

`= \hat i(0-0) -\hat j ( 0-0) +\hat k (-3* 10^5 -0.9* 10^5) \\ \\ =-3.9 * 10^5 \ k`

∴

`F^\to = q(v^\to * B^\to)`

`F^(\to) = -1.6 * 10^(-19) * -3.9 * 10^5 \\ \\ F^(\to) = 6.24 * 10^(-14 ) \ N`

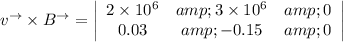
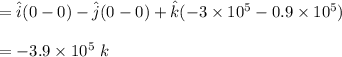
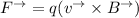
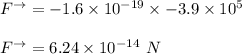
For the proton with the same velocity:

`q = 1.6 * 10^(-19 ) \ C \\ \\ F = q (v^\to * B^\to) \ \\ \\ F^\to = q(-3.9 * 10^5) \\ \\ F = (1.6 * 10^(-19)) (-3.9 * 10^5) \\ \\ \mathbf{F ^(\to) = -6.24 * 10^(-14) \ N}`