Question

Deimos's Orbit. Deimos orbits Mars at a distance of 23,460 km from the center of the planet and has a period of 1.263 days. Assume that Deimos's orbit is circular. Calculate the mass of Mars. Express your answer in units of kg. (Hint: Use the circular orbit velocity formula ; remember to use units of meters, kilograms, and seconds.) Please round the answer to four significant digits.

Answer 1

M = 5.882 10²³ kg

Step-by-step explanation:

Let's use Newton's second law to analyze the satellite orbit around Mars.

F = m a

force is universal attraction and acceleration is centripetal

a = v²/ R

the modulus of velocity in a circular orbit is constant

v= d/T

the distance of the cicule is

d =2pi R

a = 2pi R/T

we substitute

- G m M / R² = m (
`- (4\pi^2 R^2 )/(T^2 R)`)

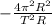G M =
`( 4\pi ^2 R^3 )/(T^2 )`

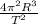
M =
`(4 \pi ^2 R^3 )/( G T^2 )`

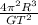
the distance R is the distance from the center of the planet Mars to the center of the satellite Deimos

R = 23460 km = 2.3460 10⁷ m

the period of the orbit is

T = 1,263 days = 1,263 day (24 h / 1 day) (3600s / h)

T = 1.0912 10⁵ s

let's calculate

M =
`(4 \pi ^2 ( 2.3460 \ 10^7)^3 )/(5.67 10^(-11) \ (1.0912 \ 10^5)^2 )`

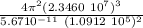
M = 509.73418 10²¹ /8.66640 10⁻¹

M = 58.817 10²² kg

M = 5.882 10²³ kg