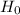Answer:
Explanation:
From the question we are told that:
Null Hypothesis
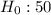
Alternative Hypothesis
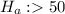
Sample size

standard deviation
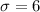
Significance level
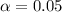
a)
Sample mean
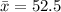
Generally the equation for Test statistics is mathematically given by
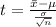
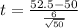
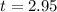
Therefore from table
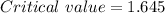
We conclude The value of test statistics is greater than critical value.
Therefore we Reject the Null hypothesis
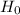
b)
Sample mean
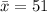
Generally the equation for Test statistics is mathematically given by
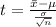


Therefore from table
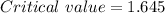
We conclude,The value of test statistics is less than critical value.
Therefore we Fail to Reject the Null hypothesis
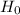
c)
Sample mean
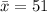
Generally the equation for Test statistics is mathematically given by
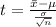
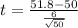

Therefore from table
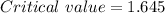
We conclude The value of test statistics is greater than critical value.
Therefore we Fail to Reject the Null hypothesis