Answer:
The surface area of the larger prism is 612.5 square meters.
Explanation:
If the two prisms are similar, then any length of the both must have the same relationship for the heights. Dimensionally speaking, we have the following expression for the surface area of the prism:
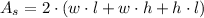 (1)
(1)
Where:
 - Surface area, in square meters.
- Surface area, in square meters.
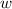 - Width, in meters.
- Width, in meters.
 - Height, in meters.
- Height, in meters.
 - Length, in meters.
- Length, in meters.
If we know that
 ,
,
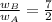 and
and
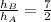 , then we get the following relationship for the volumes of the prisms:
, then we get the following relationship for the volumes of the prisms:
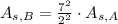 (2)
(2)
Where:
 - Surface area of the smaller prism, in square meters.
- Surface area of the smaller prism, in square meters.
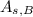 - Surface area of the greater prism, in square meters.
- Surface area of the greater prism, in square meters.
If we know that
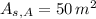 , then the surface area of the greater prism is:
, then the surface area of the greater prism is:
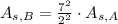
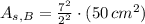
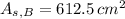
The surface area of the larger prism is 612.5 square meters.