Answer:
The candle has a radius of 8 centimeters and 16 centimeters and uses an amount of approximately 1206.372 square centimeters.
Explanation:
The volume (
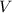 ), in cubic centimeters, and surface area (
), in cubic centimeters, and surface area (
 ), in square centimeters, formulas for the candle are described below:
), in square centimeters, formulas for the candle are described below:
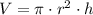 (1)
(1)
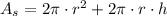 (2)
(2)
Where:
 - Radius, in centimeters.
- Radius, in centimeters.
 - Height, in centimeters.
- Height, in centimeters.
By (1) we have an expression of the height in terms of the volume and the radius of the candle:
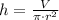
By substitution in (2) we get the following formula:
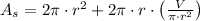

Then, we derive the formulas for the First and Second Derivative Tests:
First Derivative Test
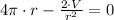
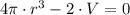
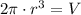
![r = \sqrt[3]{(V)/(2\pi) }](https://img.qammunity.org/2022/formulas/mathematics/college/agr5vf2az2rgokgxysqrh3nfiz0icog4n0.png)
There is just one result, since volume is a positive variable.
Second Derivative Test
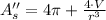
If
![\left(r = \sqrt[3]{(V)/(2\pi)}\right)](https://img.qammunity.org/2022/formulas/mathematics/college/2t6i11a3vtfj3gblnvv57x37wqpla75n3a.png) :
:
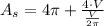
 (which means that the critical value leads to a minimum)
(which means that the critical value leads to a minimum)
If we know that
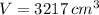 , then the dimensions for the minimum amount of plastic are:
, then the dimensions for the minimum amount of plastic are:
![r = \sqrt[3]{(V)/(2\pi) }](https://img.qammunity.org/2022/formulas/mathematics/college/agr5vf2az2rgokgxysqrh3nfiz0icog4n0.png)
![r = \sqrt[3]{(3217\,cm^(3))/(2\pi)}](https://img.qammunity.org/2022/formulas/mathematics/college/wkbo63749ccc761av54cj440xy5t85ulsm.png)

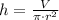
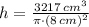
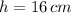
And the amount of plastic needed to cover the outside of the candle for packaging is:
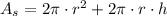

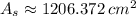
The candle has a radius of 8 centimeters and 16 centimeters and uses an amount of approximately 1206.372 square centimeters.