Question

Prove :


`\large{ \tt{ (1)/( \sec \alpha + 1 ) - \frac{ \cos\alpha }{ { \sin^(2) \alpha } } = \frac{ \cos \alpha }{ { \sin}^(2) \alpha } - (1)/( \sec \alpha - 1) }}`
*Irrelevant / Random answers will be reported!​

Answer 1

See Below.

Explanation:

We want to verify the equation:

`\displaystyle (1)/(\sec\alpha+1)-(\cos\alpha)/(\sin^2\alpha)=(\cos\alpha )/(\sin^2\alpha )-(1)/(\sec\alpha -1)`

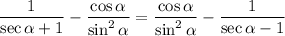
We can convert sec(α) to 1 / cos(α):

`\displaystyle (1)/(1/\cos\alpha+1)-(\cos\alpha)/(\sin^2\alpha)=(\cos\alpha )/(\sin^2\alpha )-(1)/(\sec\alpha -1)`

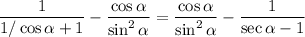
Multiply both layers of the first fraction by cos(α):

`\displaystyle (\cos\alpha)/(1+\cos\alpha)-(\cos\alpha)/(\sin^2\alpha)=(\cos\alpha )/(\sin^2\alpha )-(1)/(\sec\alpha -1)`

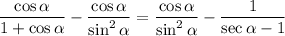
Create a common denominator. We can multiply the first fraction by (1 - cos(α)):

`\displaystyle (\cos\alpha(1-\cos\alpha))/((1+\cos\alpha)(1-\cos\alpha))-(\cos\alpha)/(\sin^2\alpha)=(\cos\alpha )/(\sin^2\alpha )-(1)/(\sec\alpha -1)`

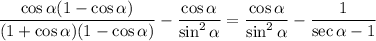
Simplify:

`\displaystyle (\cos\alpha(1-\cos\alpha))/(1-\cos^2\alpha)-(\cos\alpha)/(\sin^2\alpha)=(\cos\alpha )/(\sin^2\alpha )-(1)/(\sec\alpha -1)`

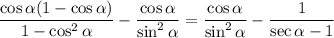
From the Pythagorean Identity, we know that cos²(α) + sin²(α) = 1 or equivalently, 1 - cos²(α) = sin²(α). Substitute:

`\displaystyle (\cos\alpha(1-\cos\alpha))/(\sin^2\alpha)-(\cos\alpha)/(\sin^2\alpha)=(\cos\alpha )/(\sin^2\alpha )-(1)/(\sec\alpha -1)`

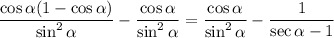
Subtract:

`\displaystyle (\cos\alpha(1-\cos\alpha)-\cos\alpha)/(\sin^2\alpha)=(\cos\alpha)/(\sin^2\alpha)-(1)/(\sec\alpha-1)`

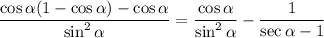
Distribute:

`\displaystyle (\cos\alpha-\cos^2\alpha-\cos\alpha)/(\sin^2\alpha)=(\cos\alpha)/(\sin^2\alpha)-(1)/(\sec\alpha-1)`

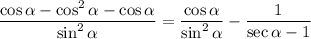
Rewrite:

`\displaystyle ((\cos\alpha)-(\cos^2\alpha+\cos\alpha))/(\sin^2\alpha)=(\cos\alpha)/(\sin^2\alpha)-(1)/(\sec\alpha-1)`

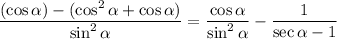
Split:

`\displaystyle (\cos\alpha)/(\sin^2\alpha)-(\cos^2\alpha+\cos\alpha)/(\sin^2\alpha)=(\cos\alpha)/(\sin^2\alpha)-(1)/(\sec\alpha-1)`

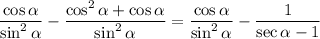
Factor the second fraction, and substitute sin²(α) for 1 - cos²(α):

`\displaystyle (\cos\alpha)/(\sin^2\alpha)-(\cos\alpha(\cos\alpha+1))/(1-\cos^2\alpha)=(\cos\alpha)/(\sin^2\alpha)-(1)/(\sec\alpha-1)`

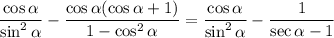
Factor:

`\displaystyle (\cos\alpha)/(\sin^2\alpha)-(\cos\alpha(\cos\alpha+1))/((1-\cos\alpha)(1+\cos\alpha))=(\cos\alpha)/(\sin^2\alpha)-(1)/(\sec\alpha-1)`

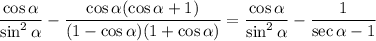
Cancel:

`\displaystyle (\cos\alpha)/(\sin^2\alpha)-(\cos\alpha)/((1-\cos\alpha))=(\cos\alpha)/(\sin^2\alpha)-(1)/(\sec\alpha-1)`

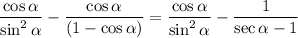
Divide the second fraction by cos(α):

`\displaystyle (\cos\alpha)/(\sin^2\alpha)-(1)/(\sec\alpha-1)=\displaystyle (\cos\alpha)/(\sin^2\alpha)-(1)/(\sec\alpha-1)`

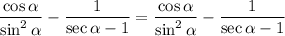
Hence proven.