Question

A fairground ride consists of a large vertical drum that spins so

fast that everyone inside it stays pinned against the wall when
the floor drops away. The diameter of the drum is 10 m. Assume
that the coefficient of static friction between the drum and the
rider’s clothes are 0.15.
a) What is the minimum speed required for the riders so that
they stay pinned against the inside of the drum when the
the floor drops away?

Answer 1

v = 3.84 m/s

Step-by-step explanation:

In order for the riders to stay pinned against the inside of the drum the frictional force on them must be equal to the centripetal force:

`Centripetal\ Force = Frictional\ Force\\\\(mv^2)/(r) = \mu R = \mu W\\\\(mv^2)/(r) = \mu mg\\\\(v^2)/(r) = \mu g\\\\v = √(\mu gr)`

where,

v = minimum speed = ?

g = acceleration due to gravity = 9.81 m/s²

r = radius = 10 m

μ = coefficient of friction = 0.15

Therefore,

`v=√((0.15)(9.81\ m/s^2)(10\ m))`

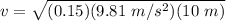
v = 3.84 m/s