Answer:
The total energy absorbed is 32.171 kilojoules.
Step-by-step explanation:
The total energy absorbed by the ice is the sum of the sensible heat of ice and water and the latent heat of fusion of the water, that is:
![Q = m\cdot [c_(i)\cdot (T_(2)-T_(1))+L_(f) + c_(w)\cdot (T_(3)-T_(2))]](https://img.qammunity.org/2022/formulas/chemistry/college/wucbcjnhw3c34cao1rnz8y2rs951f17qob.png) (1)
(1)
Where:
 - Mass of the ice, in kilograms.
- Mass of the ice, in kilograms.
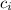 - Specific heat of ice, in kilojoules per kilogram-degree Celsius.
- Specific heat of ice, in kilojoules per kilogram-degree Celsius.
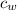 - Specific heat of water, in kilojoules per kilogram-degree Celsius.
- Specific heat of water, in kilojoules per kilogram-degree Celsius.
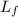 - Latent heat of fusion, in kilojoules per degree Celsius.
- Latent heat of fusion, in kilojoules per degree Celsius.
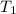 - Initial temperature of water, in degrees Celsius.
- Initial temperature of water, in degrees Celsius.
 - Fusion point of water, in degrees Celsius.
- Fusion point of water, in degrees Celsius.
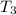 - Final temperature of water, in degree Celsius.
- Final temperature of water, in degree Celsius.
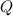 - Total energy absorbed, in kilojoules.
- Total energy absorbed, in kilojoules.
If we know that
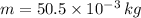 ,
,
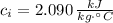 ,
,
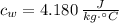 ,
,
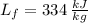 ,
,
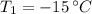 ,
,
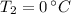 and
and
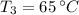 , then the total energy absorbed is:
, then the total energy absorbed is:
![Q= (50.5* 10^(-3)\,kg)\cdot \left[\left(2.090\,(kJ)/(kg\cdot ^(\circ)C) \right)\cdot (15\,^(\circ)C) + 334\,(kJ)/(kg)+ \left(4.180\,(kJ)/(kg\cdot ^(\circ)C) \right)\cdot (65\,^(\circ)C)\right]](https://img.qammunity.org/2022/formulas/chemistry/college/8vn9kl5xq7hkg28e81fkmj5c3gh6toc7mn.png)
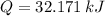
The total energy absorbed is 32.171 kilojoules.