Question

What are the solutions to the equation x2 + 4x - 5 = 0?

a. 1 and -5
b. -1 and 5
c. -5
d. -1 and -5

Answer 1

Your answer should be option a.

Answer 2

The solutions to the equation
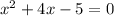`\( x^2 + 4x - 5 = 0 \)` are x = 1 and x = -5 , corresponding to option a

To find the solutions to the quadratic equation
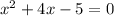`\( x^2 + 4x - 5 = 0 \)`, we can use the quadratic formula:

`\[ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}} \]`

Where:

`\( a \) is the coefficient of \( x^2 \) (which is 1),`

`- \( b \) is the coefficient of \( x \) (which is 4),`

`\( c \) is the constant term (which is -5).`

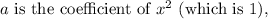
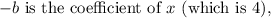
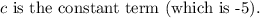
The discriminant
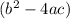`(\( b^2 - 4ac \))` will determine the nature of the roots. Here, the discriminant is
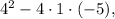`\( 4^2 - 4 \cdot 1 \cdot (-5) \),` which is positive, indicating two real and distinct solutions.

Applying the quadratic formula:

`\[ x = \frac{{-4 \pm \sqrt{{16 + 20}}}}{2} \]`

`\[ x = \frac{{-4 \pm √(36)}}{2} \]`

`\[ x = \frac{{-4 \pm 6}}{2} \]`

This gives us two solutions:

`\[ x_1 = \frac{{-4 + 6}}{2} = 1 \]`

`\[ x_2 = \frac{{-4 - 6}}{2} = -5 \]`