Question

A particle moves along the x-axis with the given acceleration function a(t) = 8t - 6, initial position s(0) = 2, and initial velocity v(0). Find the position function.

Answer 1

`s(t) = (4t^3)/(3) - 3t^2 + v(0)t + 2`

Explanation:

Relation between acceleration, velocity and position:

The velocity function is the integral of the acceleration function.

The position function is the integral of the velocity function.

Acceleration:

As given by the problem, the acceleration function is:

`a(t) = 8t - 6`

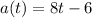
Velocity:

`v(t) = \int a(t) dt = \int (8t - 6) dt = (8t^2)/(2) - 6t + K = 4t^2 - 6t + K`

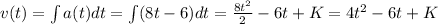
In which the constant of integration K is the initial velocity, which is v(0). So

`v(t) = 4t^2 - 6t + v(0)`

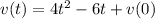
Position:

`s(t) = \int v(t) dt = \int (4t^2 - 6t + v(0)) dt = (4t^3)/(3) - (6t^2)/(2) + v(0)t + K = (4t^3)/(3) - 3t^2 + v(0)t + K`

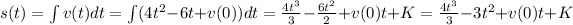
The initial position is s(0) = 2. So

`s(t) = (4t^3)/(3) - 3t^2 + v(0)t + 2`