Question

4. Find an equation of the line that is tangent to the graph of 4x + 2xy^2 +44 = y^3 at the point (-3,2).

i need this asap.

Answer 1

Given:

The equation is:

`4x+2xy^2+44=y^3`

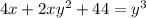
To find:

The equation of the tangent on the given equation at point (-3,2).

Solution:

We have,

`4x+2xy^2+44=y^3`

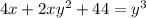
Differentiate with respect to x.

`4(1)+2[x(2yy')+y^2(1)]+0=3y^2y'`

`4+4xyy'+2y^2=3y^2y'`

`4+2y^2=3y^2y'-4xyy'`

`4+2y^2=(3y^2-4xy)y'`

Isolate y'.

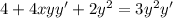
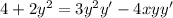
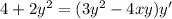
`(4+2y^2)/(3y^2-4xy)=y'`

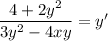
Now, we need to find the value of the derivative at point (-3,2).

`y'_((-3,2))=(4+2(2)^2)/(3(2)^2-4(-3)(2))`

`y'_((-3,2))=(4+8)/(12+24)`

`y'_((-3,2))=(12)/(36)`

`y'_((-3,2))=(1)/(3)`

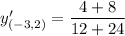
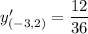
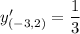
It means the slope of the tangent line is
`(1)/(3)`.

The equation of tangent line that passes through the point (-3,2) with slope
`(1)/(3)` is:

`y-y_1=m(x-x_1)`

`y-2=(1)/(3)(x-(-3))`

`y-2=(1)/(3)x+1`

`y=(1)/(3)x+1+2`

`y=(1)/(3)x+3`

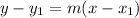
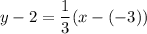
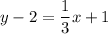
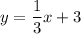
Therefore, the equation of tangent line is
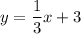`y=(1)/(3)x+3`.