Question

I need help!!

Solve the equation. Give the exact solution and an approximate solution to three decimal places.

5^(7x) = 60

Answer 1

The exact solution is

`x = (Ln(60))/(7*Ln(5))`

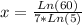
And the approximation to three decimal places is:

x = 0.363

Explanation:

Here we have the equation:

`5^(7*x) = 60\\`

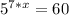
Now we can remember a property of the natural logarithm function:

Ln(a^n) = n*Ln(a)

Now we can apply the Ln( ) function to both sides of that equation to get:

`Ln(5^(7*x)) = Ln(60)`

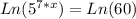
Then we get:

`7*x*Ln(5) = Ln(60)`

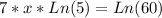
Solving that for x we get:

`x = (Ln(60))/(7*Ln(5)) = 0.363`

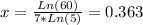
So the exact solution is:

`x = (Ln(60))/(7*Ln(5))`

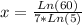
And the approximation to three decimal places is:

x = 0.363