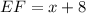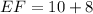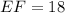Answer:
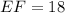
Explanation:
Given
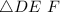 similar to
similar to
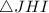
Required
Find
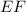
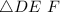 similar to
similar to
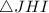 implies that:
implies that:
The corresponding sides are:
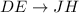
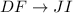

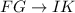
First, solve for x using the following corresponding ratios
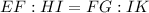
This gives:
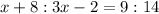
Express as fraction
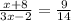
Cross multiply
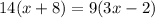
Open brackets
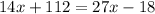
Collect like terms
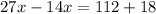
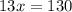
Solve for x
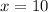
In the diagram, we have: