Given:
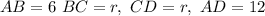 .
.
To find:
The value of r.
Solution:
We have,
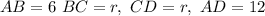 .
.
We know that the radius is perpendicular to the tangent at the point of tangency
AD is the tangent and CD is the radius. So, CD is perpendicular to AD at point D, i.e.,
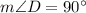 .
.
Using Pythagoras theorem, we get
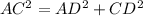
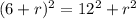
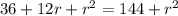
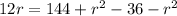
On further simplification, we get
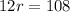

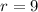
Therefore, the value of r is 9.