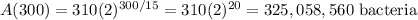Answer:
The initial population is about 310 bacteria.
The size of the bacterial population after five hours is about 325, 058, 560.
Explanation:
The exponential function describing growth is given by:
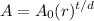
Where A is the amount afterwards, A₀ is the initial amount, r is the rate of growth, t is the amount of time that has passed and d is the time it takes for one cycle (both t and d are minutes in this case).
We are given that the bacteria population doubles after every 15 minutes. Hence, r = 2 and d = 15:
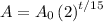
At time t = 110 minutes, the bacterial population was 50,000. Hence:

Solve for A₀:

Hence, the initial population (when t = 0) was about 310.
Thus, our function is:
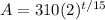
After five hours, 300 minutes would have passed. Thus: