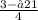Question

Solve each problem and show the work for each one.

Solve by factoring.
1. 2x^2+9x+26=-4x+5

Solve by using the quadratic formula and round to the nearest hundredth.
2. 3x^2-6x-4=0​

Answer 1

Solve by factoring.

1. 2x^2+9x+26=-4x+5

2x²+9x+4x+26-5=0

2x²+13x+21=0

doing middle term factorization

2x²+7x+6x+21=0

x(2x+7)+3(2x+7)=0

(2x+7)(x+3)=0

either

x=-7/2

or

x=-3.

2.

3x^2-6x-4=0

comparing above equation with ax²+bx+c=0

we get

a=3

b=-6

c=-4

By using quadratic equation

x=
`\frac{ - b±\sqrt{ {b}^(2) - 4ac } }{2a}`

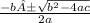
Substituting value

x=
`\frac{ 6±\sqrt{ {-6}^(2) - 4*3*-4 }}{2*-4}`

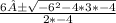
x=
`\frac{ 6±\sqrt{ {84}}}{-8}`

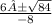
x=
`\frac{ 6±2\sqrt{ {21}}}{-8}`

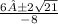
-8x=6±2√21

taking positive

-8x=6+2√21

x=
`(6+2√21)/(-8)`

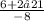
x=-
`(3+√21)/(4)`

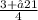
taking negative

-8x=6-2√21

x=
`(6-2√21)/(-8)`

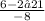
x=-
`(3-√21)/(4)`