Answer:
Our equation is:
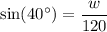
Solving this yields that the width of the river is about 77 feet.
Explanation:
Part A)
We know that McNeal is 120 feet from the tree. This is the hypotenuse.
And we want to find the width of the river, which is the side opposite from our angle.
Since we want to find the side opposite to our angle and we are given the hypotenuse, we will use the sine ratio:
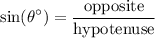
Our angle is 40°.
The opposite side is unknown. We can let this be w to represent width.
The hypotenuse is 120 feet. Hence, our equation is:
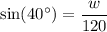
Part B)
Solve for w:
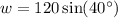
Use a calculator:
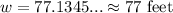
The width of the river is about 77 feet.