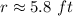Answer:
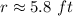
General Formulas and Concepts:
Symbols
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Equality Properties
- Multiplication Property of Equality
- Division Property of Equality
- Addition Property of Equality
- Subtraction Property of Equality
Geometry
Volume of a Sphere Formula:
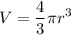
Explanation:
Step 1: Define
Identify variables
Volume V = 797 ft³
Step 2: Solve for r
- Substitute in variables [Volume of a Sphere Formula]:
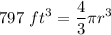
- [Division Property of Equality] Isolate r term:

- Rewrite:
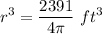
- [Equality Property] Cube root both sides:
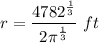
- Evaluate:
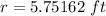
- Round: