Question

Find the missing side
length to the nearest
tenth of a foot.

Answer 1

b ~ 11.5

Explanation:

The given figure is a right triangle or a triangle that contains a right angle. The right angle is indicated by the box around one of the angles of the triangle. This means that one can use the Pythagorean theorem to find the missing side lengths. The Pythagorean states the following,

`a^2+b^2=c^2`

Where the value (a) and (b) represents the legs or the sides adjacent to the right angle of the trinalge. The side (c) represents the hypotenuse or the side opposite the right angle of the right triangle.

Substitute in the given values and solve for the unknown,

`(8)^2 +(b)^2=(14)^2\\`

Simplify,

`64+b^2=196`

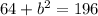
Inverse operations,

`64+b^2=196\\-64\\\\b^2=132\\\sqrt{}\\\\b=2√(33)`

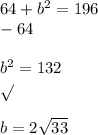
b ~ 11.5