Question

Se lanza un cuerpo verticalmente hacia arriba con una velocidad de 98 m/s. ¿Qué altura y que velocidad alcanza al cabo de 3 segundo? y ¿cuál es la altura máxima alcanzada por el cuerpo?​

Answer 1

jsjsjsjshshshsh nrnrnrnr r rn kai what he shs us is is si si siri with sis si si si si did find

Answer 2

Using the equations of motion for constant acceleration, the body reaches a height of approximately 249.855 m and a speed of approximately 68.57 m/s after 3 seconds, and it reaches a maximum height of approximately 490.33 m

The final velocity after 3 seconds using the equation:

v = u + at

Where v = final velocity

u = initial velocity

a = acceleration due to gravity (approximately -9.81 m/s^2)

t = time

u = 98 m/s

a = -9.81 m/s^2

t = 3 seconds

v = 98 - 9.81 * 3 v

≈ 98 - 29.43 v

≈ 68.57 m/s

Thus, the speed reached after 3 seconds is approximately 68.57 m/s.

The height reached after 3 seconds using the equation:

s = ut + (1/2)at^2

Where:

s = displacement (height)

u = initial velocity

t = time

a = acceleration due to gravity

u = 98 m/s

t = 3 seconds

a = -9.81 m/s^2

s = 983 + (1/2)(-9.81)*(3)^2 s

= 294 - 44.145 s

≈ 249.855 m

Thus, the height reached after 3 seconds is approximately 249.855 m.

Using the equation for the maximum height reached in a vertical motion:
`h_max = (u^2)/(2|a|)`

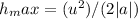
Where:

h_max = maximum height

u = initial velocity

a = acceleration due to gravity

u = 98 m/s

a = -9.81 m/s^2

`h_max = (98^2)/(2*9.81) h_{max`

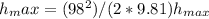
= 9604/19.62 h_max

≈ 490.33 m

Thus, the maximum height reached by the body is approximately 490.33 m.

Thus, the body reaches a height of approximately 249.855 m and a speed of approximately 68.57 m/s after 3 seconds, and it reaches a maximum height of approximately 490.33 m.

Complete Question:

A body is thrown vertically upward with a speed of 98 m/s. What height and speed does it reach after 3 seconds? And what is the maximum height reached by the body?​