Answer:
Rectangular route
Explanation:
Given
H(-4, 3) B (2, 11) F (6, 8) C (0, 0)
Required
The type of route
First, calculate the distance between adjacent points i.e. HB, BF, FC and CH
Where
HB and FC are opposite
BF and CH are opposite
Using distance formula:
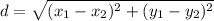
So, we have:
HB
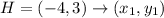
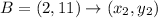
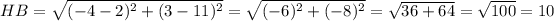
BF
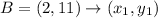
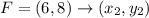
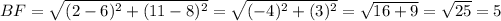
FC
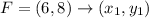
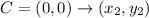
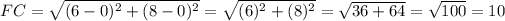
CH
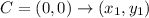
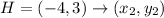
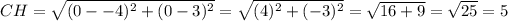
So, we have:
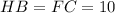

Sine the opposite sides are equal; We can conclude that the route is a rectangle