Question

Which 3 of the following numbers are irrational?

PLEASE ONLY ANSWER IF YOU KNOW THE ANSWER.


`13 + √(25)`

`17\pi`

`.21475467...`

`\sqrt{ (9 )/(16) }`

`- (4)/(5) + \sqrt{ (6)/(9) }`


​

Answer 1

The irrational numbers from the given options are :-

• 
  `17\pi`
• 
  `0.21475467.....`
• 
  `-(4)/(5) + \sqrt{(6)/(9) }`

Explanation:

Analyse each option carefully.

1)
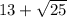`13 + √(25)` is a rational number because :-

• 
  `√(25) = 5`
• 
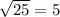
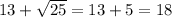  `13 + √(25) = 13 + 5 = 18` , which is a rational number.

2)
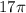`17\pi` is irrational because :-

• Value of π has a non-terminating & non-recurring decimal value. So it is irrational number.
• If π is irrational , then 17π is also irrational because product of any number and an irrational number is always irrational.

3)
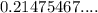`0.21475467....` is irrational because :-

• It is a non-terminating & non-recurring decimal.

• Any non terminating & non-recurring decimal is an irrational number.

4)
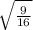`\sqrt{(9)/(16) }` is rational because :-

• 
  `\sqrt{(9)/(16) } = (√(9) )/(√(16) ) = (3)/(4)`.
• 
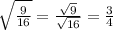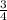  `(3)/(4)` is a rational number.

5)
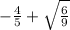`-(4)/(5) + \sqrt{(6)/(9) }` is irrational because :-

• 
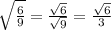  `\sqrt{(6)/(9) } = (√(6) )/(√(9) ) = (√(6) )/(3)` , which is irrational.
• If
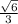  `(√(6) )/(3)` is irrational , then
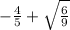  `-(4)/(5) + \sqrt{(6)/(9) }` is also irrational because sum of any number and an irrational number is always an irrational number.