Question

For the point P(25,-15) and Q​(30,-12), find the distance​ d(P,Q) and the coordinates of the midpoint M of the segment PQ.

Answer 1

`d(P,Q) = √(34)`

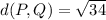
The midpoint of the segment is M(27.5, -13.5).

Explanation:

Distance between two points:

Suppose that we have two points,
`(x_1,y_1)` and
`(x_2,y_2)`. The distance between them is given by:

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

Distance between P(25,-15) and Q​(30,-12)

`d(P,Q) = √((30-25)^2+(-12-(-15))^2) = √(34)`

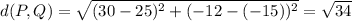
So

`d(P,Q) = √(34)`

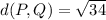
Coordinates of the midpoint M of the segment PQ.

Mean of the coordinates of P and Q. So

`x_M = (25+30)/(2) = (55)/(2) = 27.5`

`y_M = (-15-12)/(2) = -(27)/(2) = -13.5`

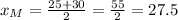
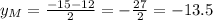
The midpoint of the segment is M(27.5, -13.5).