Answer:
Explanation:
Equation of the line y = mx + c
The new line is perpendicular to 2x - 3y = -5
- 3y = - 5 - 2x
3y = 2x + 5
y =

Since the lines are perpendicular to each other :
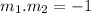
where
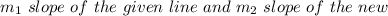 .
.
Slope of the given line
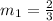
Slope of the new line

The equation to the new line passing through (-4, -3) and perpendicular to 2x - 3y = -5
