Question

To find this take the average of the absolute values of the differences between each member of a data set in the mean of the data set

Answer 1

The phrase describes a statistical measure called the mean absolute deviation

The description you provided is defining the mean absolute deviation (MAD) of a data set. The mean absolute deviation is a measure of the spread or dispersion of a set of values. To calculate the MAD, you follow these steps:

Find the mean (average) of the data set.

Calculate the absolute difference between each data point and the mean.

Find the average of these absolute differences.

Mathematically, MAD is often expressed using the formula:

`M = (1)/(n) \sum |x_i - mean|`

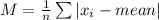
Complete question:

"To find this take the average of the absolute values of the differences between each member of a data set in the mean of the data set

What it is?"

Answer 2

See Explanation

Explanation:

The question is incomplete, as the dataset is missing; However, one can deduce that the question implies that you calculate the mean absolute deviation of the missing dataset.

Take for instance, the dataset is: 1, 2, 2, 3, 3, 5, 8

Calculate the mean:

`\bar x = (\sum x)/(n)`

`\bar x = (1+2+2+3+3+5+8)/(7)`

`\bar x = (24)/(7)`

`\bar x = 3.43`

Next, proceed to the instruction in the question;

Which is:

`M = (1)/(n)\sum\limits^(n)_(i=1)|x_i - \bar x|`

So, we have:

`M = (1)/(7)(|1-3.43| + |2 - 3.43| + |2 - 3.43| + |3 - 3.43| + |3 - 3.43| + |5 - 3.43| + |8 - 3.43|)`

`M = (1)/(7)(|-2.43| + |- 1.43| + |-1.43| + |- 0.43| + |-0.43| + |1.57| + |4.57|)`

Remove absolute brackets

`M = (1)/(7)(2.43 + 1.43 + 1.43 + 0.43 + 0.43 + 1.57 + 4.57)`

`M = (1)/(7)*12.29`

`M = 1.76`