Question

The square based pyramid whose length of side of square base and slant height are in the ratio 6:5 and volume is 48000cm^3 .Find the total surface area

Answer 1

`A=9600cn^2`

Explanation:

From the question we are told that:

Ratio of square base and slant height
`R=6:5`

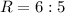
Volume
`V=48000cm^3`

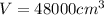
Generally the equation for height Pyramid h is mathematically given by

`h^2=s^2+((1)/(2)a^2)`

`h=\sqrt{s^2+((1)/(2)a)^2)}`

`h=√(5^2+3^2)`

`h=4`

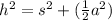
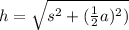
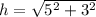
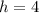
Where

a= base Length

s=slant height of pyramid

Therefore the ratio of height is

`h=4`

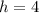
Generally the equation for The Volume of Square based Pyramid V is mathematically given by

`V=a^2(h)/(3)`

`V=6^2(4)/(3)`

`V=48`

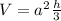
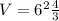
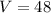
Therefore the ratio of volume is

V=48

Generally for V=4800

Therefore

`a=60`

`h=40`

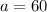
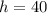
Generally the equation for Area of Square based Pyramid A is mathematically given by

`A=a^2+2a\sqrt{(a^2)/(4)+h^2 }`

`A=60^2+2(60)\sqrt{((60)^2)/(4)+(40)^2}`

`A=9600cn^2`

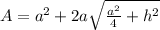
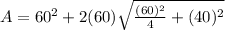
Therefore the Area of Square based Pyramid A is

`A=9600cn^2`