Answer:
d = 4.425 x 10⁻⁶ m = 4.425 μm
Step-by-step explanation:
The charge on plates can be given as:

where,
d = spacing between plates = ?
ε₀ = Permitivity of free space = 8.85 x 10⁻¹² C²/Nm²
σ = surface charge density = (30 nC/cm²)(10⁻⁹ C/1 nC)(1 cm²/10⁻⁴ m²)
σ = 3 x 10⁻⁴ C/m²
V = Potential Difference = 150 V
Therefore,
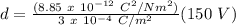
d = 4.425 x 10⁻⁶ m = 4.425 μm