Question

Find any domain restrictions on f(g(x))
f(x)= square root x-3 and g(x)=x+5

Answer 1

`x \ge -2`

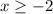
Explanation:

The "argument" of a square root (the quantity you're finding the square root of) must be greater than or equal to 0.

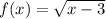`f(x)=√(x-3)` requires
`x-3 \ge 0 \Rightarrow x \ge 3`.

But in the function f(g(x)), the input to f is g(x) = x + 5, so x + 5 must be greater than or equal to 3.

`x+5 \ge 3 \Rightarrow x\ge -2`

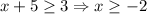
Composite functions can be confusing; one reason is the use of the same symbol, x to represent numbers from the domain of EACH function. See if it helps to call the domain of g by the name x, and the domain of f by some other name.

`f(z)=√(z-3)\\g(x)=x+5\\f(g(x))=f(x+5)=√((x+5)-3)=√(x+2)`

The square root will require
`x+2 \ge 0 \Rightarrow x \ge -2`