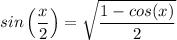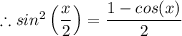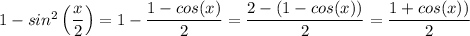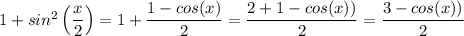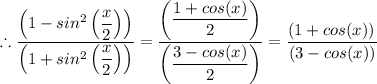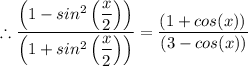Question

Verify that each equation is an identity (1 - sin^(2)((x)/(2)))/(1+sin^(2)((x)/(2)))= (1+cosx)/(3-cosX)

Answer 1

Given that we have;

`sin \left ((x)/(2) \right ) = \sqrt{(1 - cos (x))/(2) }`

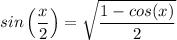
By the application of the law of indices and algebraic process of adding a and subtracting a fraction from a whole number, we have;

`\therefore (\left ( 1 - sin^2 \left ((x)/(2) \right ) \right ))/(\left ( 1 + sin^2 \left ((x)/(2) \right ) \right )) =(\left ( (1 + cos (x))/(2) \right))/(\left ((3 - cos (x))/(2) \right ) ) =(\left ( 1 + cos (x)))/((3 - cos (x)))`

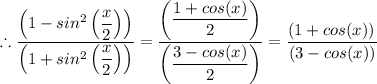
Explanation:

An identity is a valid or true equation for all variable values

The given equation is presented as follows;

`(\left ( 1 - sin^2 \left ((x)/(2) \right ) \right ))/(\left ( 1 + sin^2 \left ((x)/(2) \right ) \right )) =(\left ( 1 + cos (x)))/((3 - cos (x)))`

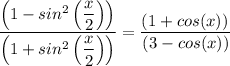
From trigonometric identities, we have;

`sin \left ((x)/(2) \right ) = \sqrt{(1 - cos (x))/(2) }`

`\therefore sin^2 \left ((x)/(2) \right ) = (1 - cos (x))/(2)`

`1 - sin^2 \left ((x)/(2) \right ) = 1 - (1 - cos (x))/(2) = (2 - (1 - cos (x)))/(2) = (1 + cos (x)))/(2)`

`1 + sin^2 \left ((x)/(2) \right ) = 1 + (1 - cos (x))/(2) = (2 + 1 - cos (x)))/(2) = (3 - cos (x)))/(2)`

`\therefore (\left ( 1 - sin^2 \left ((x)/(2) \right ) \right ))/(\left ( 1 + sin^2 \left ((x)/(2) \right ) \right )) =(\left ( (1 + cos (x))/(2) \right))/(\left ((3 - cos (x))/(2) \right ) ) =(\left ( 1 + cos (x)))/((3 - cos (x)))`

`\therefore (\left ( 1 - sin^2 \left ((x)/(2) \right ) \right ))/(\left ( 1 + sin^2 \left ((x)/(2) \right ) \right )) =(\left ( 1 + cos (x)))/((3 - cos (x)))`