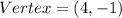Question

) () = 2 − 6 + 13 Translate f(x) 7 units to the left and down 5 units. Write your new function in vertex form

Answer 1

`y= (x -4)^2 - 1`

`Vertex = (4,-1)`

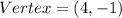
Explanation:

Given

`f(x) = x^2 + 6x+13`

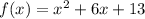
Required

7 units left and 5 units down

First, we have: [7 units left]

The rule is:

`(x,y) \to (x-7,y)`

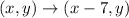
So, we have:

`f(x) = (x - 7)^2 + 6(x -7)+13`

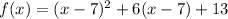
Next, we have: [5 units down]

The rule is:

`(x,y) \to (x,y-5)`

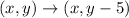
So, we have:

`f'(x) = (x - 7)^2 + 6(x -7)+13 - 5`

`f'(x) = (x - 7)^2 + 6(x -7)+8`

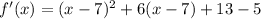
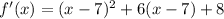
Rewrite as:

`y = (x - 7)^2 + 6(x -7)+8`

Expand

`y = x^2 - 14x + 49 + 6x -42+8`

Collect like terms

`y = x^2 - 14x + 6x -42+8+ 49`

`y = x^2 -8x +15`

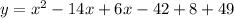
To write in vertex form, we have

Subtract 15 from both sides

`y -15= x^2 -8x`

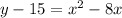
Divide (-8) by 2; Add the square to both sides

`y -15+ (-8/2)^2= x^2 -8x + (-8/2)^2`

`y -15+ 16= x^2 -8x + 16`

`y +1= x^2 -8x + 16`

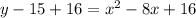
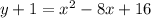
Expand

`y +1= x^2 -4x - 4x + 16`

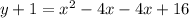
Factorize

`y +1= x(x -4) -4(x - 4)`

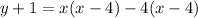
Factor out x - 4

`y +1= (x -4)(x - 4)`

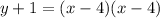
Rewrite as:

`y +1= (x -4)^2`

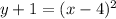
Make y the subject

`y= (x -4)^2 - 1`

The vertex is:

`Vertex = (4,-1)`