Question

Write down and simplify all the terms in the expansion of (1+3x)6.Using your results to estimate the value of (0.97)6correct to four decimal places

Answer 1

`(a)\ (1 + 3x)^6 = 728x^6 + 1458x^5 + 1215x^4 + 540x^3 + 135x^2 + 18x + 1`

`(b)\ (1 + 3(-0.01))^6 = 0.8330`

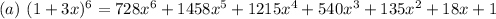
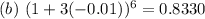
Explanation:

Given

`(1 + 3x)^6`

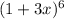
Solving (a): Expand

To do this, we make use of pascal triangle

When the exponent is 6, the factors are: 1, 6, 15, 20, 15, 6 and 1

As a rule, the exponent of 1 will start from 0 and then increase by 1 in each term while the exponent of 3x will start from 6 and then decrease by 1 in each term.

So, we have:

`(1 + 3x)^6 = 1 * 1^0 * (3x)^6 + 6 * 1^1 * (3x)^5 + 15 * 1^2 * (3x)^4 + 20 * 1^3 * (3x)^3 + 15 * 1^4 * (3x)^2 + 6 * 1^5 * (3x)^1 + 1 * 1^6 * (3x)^0`

Expand

`(1 + 3x)^6 = 1 * (3x)^6 + 6 * (3x)^5 + 15 * (3x)^4 + 20 * (3x)^3 + 15 * (3x)^2 + 6 * (3x)^1 + 1 * (3x)^0`

`(1 + 3x)^6 = 1 * 728x^6 + 6 * 243x^5 + 15 * 81x^4 + 20 * 27x^3 + 15 * 9x^2 + 6 * 3x + 1`

`(1 + 3x)^6 = 728x^6 + 1458x^5 + 1215x^4 + 540x^3 + 135x^2 + 18x + 1`

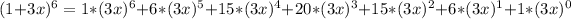
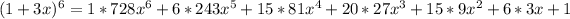
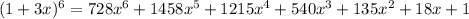
Solving (b): (0.97)^6

Rewrite as:

`(0.97)^6 = (1 - 0.03)^6`

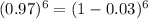
Express -0.03 as 3 * -0.01

`(0.97)^6 = (1 + 3(-0.01))^6`

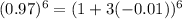
So, by comparing:

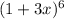`(1 + 3x)^6` and
`(1 + 3(-0.01))^6`

`x = -0.01`

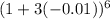
Recall that:

`(1 + 3x)^6 = 728x^6 + 1458x^5 + 1215x^4 + 540x^3 + 135x^2 + 18x + 1`

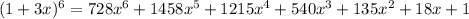
This gives:

`(1 + 3(-0.01))^6 = 728(-0.01)^6 + 1458(-0.01)^5 + 1215(-0.01)^4 + 540(-0.01)^3 + 135(-0.01)^2 + 18(-0.01) + 1`

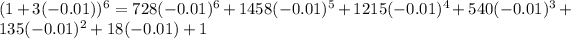
Using a calculator

`(1 + 3(-0.01))^6 = 0.000000000728 -0.0000001458+ 0.00001215 -0.00054 + 0.0135 -0.18 + 1`

`(1 + 3(-0.01))^6 = 0.83297200492`

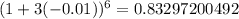
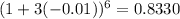`(1 + 3(-0.01))^6 = 0.8330` --- approximated