Question

The volume of this right circular cylinder is 64π cubic yards. If h, the height of the cylinder, is 4 yards, what is r, the radius of the base?

Answer 1

• Height=h=4

`\\ \rm\rightarrowtail V=\pi r^2h`

`\\ \rm\rightarrowtail 64\pi=4\pi r^2`

`\\ \rm\rightarrowtail 4r^2=64`

`\\ \rm\rightarrowtail r^2=16`

`\\ \rm\rightarrowtail r=4`

Answer 2

4 yards

Explanation:

The formula to determine the volume of the cylinder is the area of the circle (base of cylinder) multiplied by the height of the cylinder.

`\rightarrow \pi r^(2) h = \text{Volume of cylinder}`

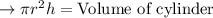
Substitute the height and the volume of the cylinder into the formula:

`\rightarrow \pi r^(2) h = \text{Volume of cylinder}`

`\rightarrow \pi (r^(2))( 4) = 64\pi`

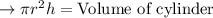
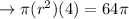
Divide both sides by π and simplify:

`\rightarrow (\pi (r^(2))( 4))/(\pi ) = (64\pi)/(\pi )`

`\rightarrow { (r^(2))( 4)} = 64`

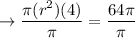
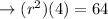
Divide both sides by 4 and simplify:

`\rightarrow { ((r^(2))( 4))/(4) } = (64)/(4)`

`\rightarrow {{(r^(2)) = 16`

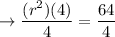
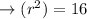
Take square root both sides and simplify:

`\rightarrow \sqrt{r^(2)} = √(16)`

`\rightarrow √(r * r) = √(4 * 4)`

`\rightarrow r = 4 \ \text{yards}`

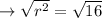
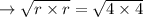
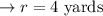
The radius of the base is 4 yards.