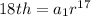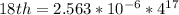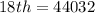Question

For a given geometric sequence, the 9th term, a9, is equal to 43/256 and the 14th term, a14, is equal to 172. Find the value of the 18 term

Answer 1

`18th=44032`

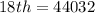
Explanation:

From the question we are told that:

9th term
`a9=(43)/(256)`

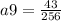
14th term
`a14=172`

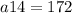
Generally the equation for Geometric sequence is mathematically given by

`a_n=a_1r^(n-1)`

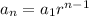
For 9th term

`(43)/(256)=a_1r^(8)`

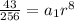
For 14th term

`172=a_1r^(13) \\a_1=(172)/(r^13)`

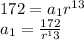
Substitute in 9th term

`(43)/(256)=(172)/(r^13)*r^(8)`

`(43)/(256*172)=r^(-5)`

`r=^5sqrt{(44032)/(43)}`

`r=4`

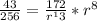
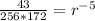
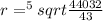
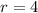
Therefore First term a is given as

`a_1=(172)/(4^13)`

`a_1=2.563*10^(-6)`

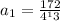
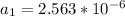
Generally the equation for the 18th term is mathematically given by

`18th=a_1r^(17)`

`18th=2.563*10^(-6)*4^(17)`

`18th=44032`