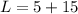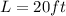Question

The length of a rectangle flower bed is 5ft longer than its width. A sidewalk with a width of 3ft surrounds the bed. If the total area of the bed and sidewalk is 546ft^2, what are the dimensions of the flower bed ?

Answer 1

`W=15ft`

`L=20ft`

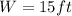
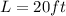
Explanation:

From the question we are told that:

Length of Bed
`L=5+W`

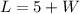
Width of sidewalk
`W_s=3ft`

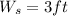
Area of the bed and sidewalk
`A_t= 546ft^2`

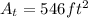
Generally the equation for Area of the bed and sidewalk
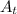`A_t` is mathematically given by

`Area=L*B`

`A_t=((3+3)+L)*((3+3)+W)`

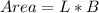
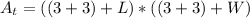
Therefore

`546=((3+3)+(5+W))*((3+3)+W)`

`0=((6+(5+W))*((6)+W)-546`

`(11+W)*(6+W)-546=0`

`W^2+17B-480=0`

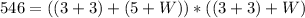
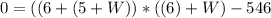
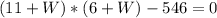
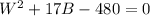
Solving the Quadratic Equation

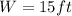`W=15ft` (Using only positive root)

Generally the Length L is mathematically given by

`L=5+15`

`L=20ft`