Answer:
21.1cm
Explanation:
Hello :)
The volume of a sphere can be found by this equation:
 where V stands for volume and r stands for the radius in the sphere.
where V stands for volume and r stands for the radius in the sphere.
Since the volume is actually given to us and we need to find the radius, we can substitute in the numbers we know, and isolate the variable we are trying to find so we can get a concise answer.

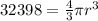
Now, let's isolate the r variable by dividing 4/3 and pi to the other side.
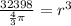
We can get rid of the exponent by square rooting by 3.
![\sqrt[3]{(32398)/((4)/(3)\pi)} =r](https://img.qammunity.org/2022/formulas/mathematics/high-school/71ejj2nwmzoxvuvdjo1nl3gj083uxo73cq.png)
If we plug this into the calculator, the r=21.1
Which means the radius of the sphere is 21.1 cm.