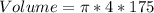Answer:

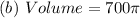
Explanation:
Given
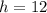
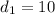 --- lower diameter
--- lower diameter
 --- upper diameter
--- upper diameter
Solving (a): The curved surface area
This is calculated as:
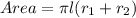
Where
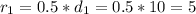 --- lower radius
--- lower radius
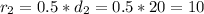 --- upper radius
--- upper radius
And
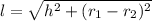 ---- l represents the slant height of the frustrum
---- l represents the slant height of the frustrum
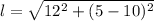

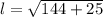
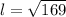
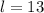
So, we have:
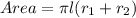


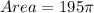
Solving (b): The volume
This is calculated as:
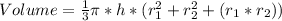
This gives: