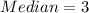Question

Kaden works 5 days. The median number of hours he works is 3. The mean number of hours he works is 4.

Answer 1

(a) 1, 2, 3, 6, 8

Explanation:

Given

`Median = 3`

`Mean = 4`

Required

The sequence of hours worked each day

See attachment for options

From the question, we understand that:

`Median = 3`

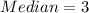
This means that, the middle number is 3 (when sorted)

So, we can conclude that (b) and (c) cannot be true because their middle numbers are 6 and 5 respectively

Next, is to determine the mean of (a) and (d)

The mean of a data is calculated as:

`\bar x = (\sum x)/(n)`

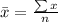
So, we have:

(a)

`\bar x = (1+ 2+ 3+ 6+ 8)/(5)`

`\bar x = (20)/(5)`

`\bar x = 4`

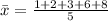
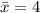
(d)

`\bar x = (1+ 2+ 3+ 4+ 5)/(5)`

`\bar x = (15)/(5)`

`\bar x = 3`

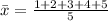
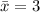
Option (a) is true, because it has:

`Median = 3`

`Mean = 4`