Question

a group of astronauts launched a model rocket from a platform. Its flight path is modeled by h= -4t^2+24t+13 where h is the height of the rocket above the ground in meters, and t is the time after the launch in seconds. How many seconds did the model rocket stay above the ground since it left the platform

Answer 1

First find where height is = 0 because once it dips below 0 then it will be below ground.
So 0 = -4t^2+24t+13
Find roots:
0=(2t-13)(2t+1)
t= -0.5 or 6.5 and cause we can’t have negative seconds
T= 6.5

Answer 2

6.5 seconds

Explanation:

Keep in mind that when
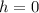`h=0`, this is the same height for both when the model rocket takes off and lands, so when the rocket lands, time is positive. Thus:

`h=-4t^2+24t+13\\\\0=-4t^2+24t+13\\\\t=(-b\pm√(b^2-4ac))/(2a)\\ \\t=(-24\pm√(24^2-4(-4)(13)))/(2(-4))\\ \\t=(-24\pm√(576+208))/(-8)\\\\t=(-24\pm√(576+208))/(-8)\\\\t=(-24\pm√(784))/(-8)\\\\t=(-24\pm28)/(-8)\\\\t=(-24-28)/(-8)\\ \\t=(-52)/(-8)\\ \\t=(52)/(8)\\\\t=6.5`

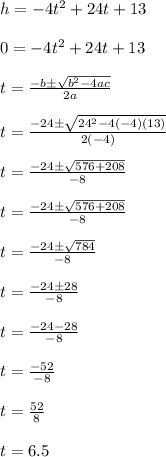
So, the amount of seconds that the model rocket stayed above the ground since it left the platform is 6.5 seconds