Question

If f(x)=x^3-4x^2-37x+40f(x)=x 3 −4x 2 −37x+40 and f(8)=0f(8)=0, then find all of the zeros of f(x)f(x) algebraically.

Answer 1

Given:

The function is:

`f(x)=x^3-4x^2-37x+40`

`f(8)=0`

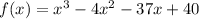
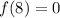
To find:

The all of the zeros of f(x) algebraically.

Solution:

We have,
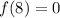`f(8)=0` is means 8 is a zero of given function and (x-8) is a factor of given function.

The function is:

`f(x)=x^3-4x^2-37x+40`

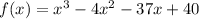
Spittle the middle terms in such a way so that we get (x-8) as a common factor.

`f(x)=x^3-8x^2+4x^2-32x-5x+40`

`f(x)=x^2(x-8)+4x(x-8)-5(x-8)`

`f(x)=(x^2+4x-5)(x-8)`

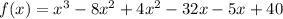
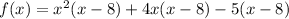
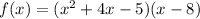
Spittle the middle term of the quadratic expression, we get

`f(x)=(x^2+5x-x-5)(x-8)`

`f(x)=(x(x+5)-1(x+5))(x-8)`

`f(x)=(x+5)(x-1)(x-8)`

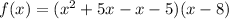
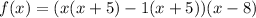
For zeros,
`f(x)=0`.

`(x+5)(x-1)(x-8)=0`

`(x+5)=0\text{ and }(x-1)=0\text{ and }(x-8)=0`

`x=-5\text{ and }x=1\text{ and }x=8`

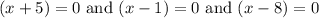
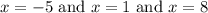
Therefore, the all zeros of the given function are -5, 1 and 8.