Question

In circle M with m \angle LMN= 46m∠LMN=46 and LM=7LM=7 units, find the length of arc LN. Round to the nearest hundredth.

Answer 1

l = 5.62 units

Explanation:

The formula for measuring the length of an arc is expressed as;

`l = r \theta`

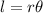
r is the radius

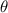`\theta` is the central angle in radians

r = LM = 7units

`\theta = (46 \pi)/(180) \\\theta = (23 \pi)/(90) \\`

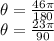
Substitute into the formula

`l = 7 * (23 \pi)/(90) \\l = 7 * (23 * 3.14)/(90) \\l = 7 * 0.8024\\l = 5.62 units`

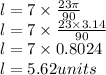
Hence the length of arc LN is 5.62 units to the nearest hundredth