Answer:
Density = 3 x 10⁻⁵ kg/m³
Step-by-step explanation:
First, we will find the volume of the planet:
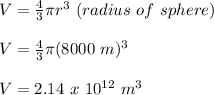
Now, we will use the expression for gravitational force to find the mass of the planet:
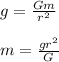
where,
m = mass = ?
g = acceleration due to gravity = 6.67 x 10⁻¹¹ m/s²
G = Universal Gravitational Constant = 6.67 x 10⁻¹¹ Nm²/kg²
r = radius = 8000 m
Therefore,
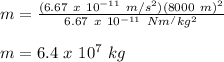
Therefore, the density will be:
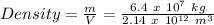
Density = 3 x 10⁻⁵ kg/m³