Question

Find the derivative of

`y = \sqrt[3]{x}`
at the point where x = 27.​

Answer 1

`\displaystyle y'(27) = (1)/(27)`

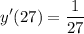
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Exponential Rule [Root Rewrite]:
  `\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`
• Exponential Rule [Rewrite]:
  `\displaystyle b^(-m) = (1)/(b^m)`

Calculus

Derivatives

Derivative Notation

Basic Power Rule

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Explanation:

Step 1: Define

y = ∛x

x = 27

Step 2: Differentiate

1. [Function] Rewrite [Exponential Rule - Root Rewrite]:
   `\displaystyle y = x^{(1)/(3)}`
2. Basic Power Rule:
   `\displaystyle y' = (1)/(3)x^{(1)/(3) - 1}`
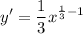
3. Simplify:
   `\displaystyle y' = (1)/(3)x^{-(2)/(3)}`
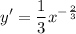
4. Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle y' = \frac{1}{3x^{(2)/(3)}}`

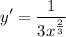
Step 3: Solve

1. Substitute in x [Derivative]:
   `\displaystyle y'(27) = \frac{1}{3(27)^{(2)/(3)}}`
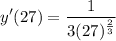
2. Evaluate exponents:
   `\displaystyle y'(27) = (1)/(3(9))`
3. Multiply:
   `\displaystyle y'(27) = (1)/(27)`

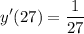
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Derivatives

Book: College Calculus 10e